I like to play. I especially enjoy playing with things that end up being useful. I started out exploring Conky when I saw this thread in the Ubuntu Forums. For those unfamiliar with the program, Conky is a lightweight system monitor that displays output to your desktop. It is highly configurable. Here’s a little sample, using some colors from the Ubuntu palette.
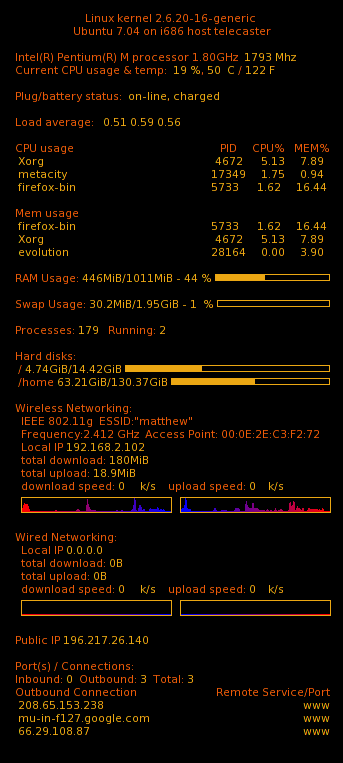
I made this by installing Conky, and then creating a hidden file in my /home called .conkyrc with the following contents.
# set to yes if you want Conky to be forked in the background background no cpu_avg_samples 2 net_avg_samples 2 out_to_console no # Use double buffering (reduces flicker, may not work for everyone) double_buffer yes # Create own window instead of using desktop (required in nautilus) own_window yes own_window_type override own_window_transparent yes own_window_hints undecorated,below,sticky,skip_taskbar,skip_pager #own_window no #own_window_transparent no # Use Xft? use_xft yes # Xft font when Xft is enabled xftfont Liberation Mono Italic:size=8 uppercase no # Text alpha when using Xft xftalpha 0.8 # Update interval in seconds update_interval 1 # Draw shades? draw_shades no # Draw outlines? draw_outline no # Draw borders around text draw_borders no # Stippled borders? stippled_borders 10 # border margins border_margin 4 # border width border_width 1 # Text alignment, other possible values are commented #minimum_size 10 10 gap_x 13 gap_y 45 #alignment top_left alignment top_right #alignment bottom_left #alignment bottom_right # Add spaces to keep things from moving about? This only affects certain objects. use_spacer yes # Subtract file system buffers from used memory? no_buffers yes TEXT ${alignc}${color #EB5B08}$sysname kernel $kernel ${alignc}${color #EB5B08}${exec cat /etc/issue.net} on $machine host $nodename ${color #EB5B08}${execi 1000 cat /proc/cpuinfo | grep 'model name' | sed -e 's/model name.*: //'} ${color #EBA713} ${freq_dyn}Mhz ${color #EB5B08}Current CPU usage & temp:${color #EBA713} ${cpu}%${color #EB5B08}, ${color #EBA713}${acpitemp}C ${color #EB5B08}/${color #EBA713} ${acpitempf}F ${color #EB5B08}Plug/battery status:${color #EBA713} $acpiacadapter, $battery ${color #EB5B08}Load average:${color #EBA713} $loadavg ${color #EB5B08}CPU usage ${alignr}PID CPU% MEM% ${color #EBA713} ${top name 1}${alignr}${top pid 1} ${top cpu 1} ${top mem 1} ${color #EBA713} ${top name 2}${alignr}${top pid 2} ${top cpu 2} ${top mem 2} ${color #EBA713} ${top name 3}${alignr}${top pid 3} ${top cpu 3} ${top mem 3} ${color #EB5B08}Mem usage ${color #EBA713} ${top_mem name 1}${alignr}${top_mem pid 1} ${top_mem cpu 1} ${top_mem mem 1} ${color #EBA713} ${top_mem name 2}${alignr}${top_mem pid 2} ${top_mem cpu 2} ${top_mem mem 2} ${color #EBA713} ${top_mem name 3}${alignr}${top_mem pid 3} ${top_mem cpu 3} ${top_mem mem 3} ${color #EB5B08}RAM Usage:${color #EBA713} $mem/$memmax - $memperc% $membar ${color #EB5B08}Swap Usage:${color #EBA713} $swap/$swapmax - $swapperc% ${swapbar} ${color #EB5B08}Processes:${color #EBA713} $processes ${color #EB5B08}Running:${color #EBA713} $running_processes ${color #EB5B08} ${color #EB5B08}Hard disks: / ${color #EBA713}${fs_used /}/${fs_size /} ${fs_bar /} ${color #EB5B08}/home ${color #EBA713}${fs_used /home}/${fs_size /home} ${fs_bar /home} ${color #EB5B08}Wireless Networking: ${color #EB5B08}${exec iwconfig eth1 | grep "ESSID" | cut -c 11-} ${color #EB5B08}${exec iwconfig eth1 | grep "Frequency" | cut -c 25-} ${color #EB5B08}Local IP ${color #EBA713}${addr eth1} ${color #EB5B08} ${color #EB5B08}total download: ${color #EBA713}${totaldown eth1} ${color #EB5B08}total upload: ${color #EBA713}${totalup eth1} ${color #EB5B08}download speed: ${color #EBA713}${downspeed eth1} k/s${color #EBA713} ${color #EB5B08} upload speed: ${color #EBA713}${upspeed eth1} k/s ${color #EBA713}${downspeedgraph eth1 15,150 ff0000 0000ff} $alignr${color #EBA713}${upspeedgraph eth1 15,150 0000ff ff0000} ${color #EB5B08}Wired Networking: ${color #EB5B08}Local IP ${color #EBA713}${addr eth0} ${color #EB5B08} ${color #EB5B08}total download: ${color #EBA713}${totaldown eth01} ${color #EB5B08}total upload: ${color #EBA713}${totalup eth0} ${color #EB5B08}download speed: ${color #EBA713}${downspeed eth0} k/s${color #EBA713} ${color #EB5B08} upload speed: ${color #EBA713}${upspeed eth0} k/s ${color #EBA713}${downspeedgraph eth0 15,150 ff0000 0000ff} $alignr${color #EBA713}${upspeedgraph eth0 15,150 0000ff ff0000} ${color #EB5B08}Public IP ${color #EBA713}${execi 3600 curl 'http://www.whatismyip.org'} ${color #EB5B08}Port(s) / Connections: ${color #EB5B08}Inbound: ${color #EBA713}${tcp_portmon 1 32767 count} ${color #EB5B08}Outbound: ${color #EBA713}${tcp_portmon 32768 61000 count} ${color #EB5B08}Total: ${color #EBA713}${tcp_portmon 1 65535 count} ${color #EB5B08}Outbound Connection ${alignr} Remote Service/Port${color #EBA713} ${tcp_portmon 32768 61000 rhost 0} ${alignr} ${tcp_portmon 32768 61000 rservice 0} ${tcp_portmon 32768 61000 rhost 1} ${alignr} ${tcp_portmon 32768 61000 rservice 1} ${tcp_portmon 32768 61000 rhost 2} ${alignr} ${tcp_portmon 32768 61000 rservice 2} ${tcp_portmon 32768 61000 rhost 3} ${alignr} ${tcp_portmon 32768 61000 rservice 3} ${tcp_portmon 32768 61000 rhost 4} ${alignr} ${tcp_portmon 32768 61000 rservice 4} ${tcp_portmon 32768 61000 rhost 5} ${alignr} ${tcp_portmon 32768 61000 rservice 5}
One of my favorite things with Conky is that I can write a shell script and have Conky execute it, like using this .conkyrc for a weather report, combined with the script that follows.
# set to yes if you want Conky to be forked in the background background no cpu_avg_samples 2 net_avg_samples 2 out_to_console no # Use double buffering (reduces flicker, may not work for everyone) double_buffer yes # Create own window instead of using desktop (required in nautilus) own_window yes own_window_type override own_window_transparent yes own_window_hints undecorated,below,sticky,skip_taskbar,skip_pager #own_window no #own_window_transparent no # Use Xft? use_xft yes # Xft font when Xft is enabled xftfont Liberation Mono Italic:size=8 uppercase no # Text alpha when using Xft xftalpha 0.8 # Update interval in seconds update_interval 1 # Draw shades? draw_shades no # Draw outlines? draw_outline no # Draw borders around text draw_borders no # Stippled borders? stippled_borders 10 # border margins border_margin 4 # border width border_width 1 # Text alignment, other possible values are commented #minimum_size 10 10 gap_x 13 gap_y 40 #alignment top_left #alignment top_right alignment bottom_left #alignment bottom_right # Add spaces to keep things from moving about? This only affects certain objects. use_spacer yes # Subtract file system buffers from used memory? no_buffers yes TEXT ${color #EB5B08}Local weather: ${color #EBA713} ${execi 1800 /home/matt/conky/weather.sh MOXX0003}
Script:
#!/bin/sh # # Grab weather data from weather.com and format it according to the given XSLT # Script written by boojit # Modified by Hellfire # Modified again by matthew # The orignal script and xslt can be downloaded from # Usage: # ${execi 1800 /path/to/weather/weather.sh location} # Usage example (Fes, Morocco): # ${execi 1800 /home/user/weather/weather.sh MOXX0003} # your Location ID: use to find it # U.S. users can just use their zip code; doubt that works for anyone else though (YMMV) LOCID=$1 # s=standard units, m=metric units UNITS=s # where this script and the XSLT lives RUNDIR=/home/matt/conky # there's probably other stuff besides CURL that will work for this, but i haven't # tried any others. # you can get curl at http://curl.haxx.se/ CURLCMD=/usr/bin/curl # get it at http://xmlsoft.org/XSLT/ XSLTCMD=/usr/bin/xsltproc # you probably don't need to modify anything below this point.... # CURL url. Use cc=* for current forecast or dayf=10 to get a multi-day forecast CURLURL="http://xoap.weather.com/weather/local/$LOCID?cc=*&unit=$UNITS&dayf=2" # The XSLT to use when translating the response from weather.com # You can modify this xslt to your liking XSLT=$RUNDIR/weather.xslt #filter (if you want to convert stuff to lower-case or upper case or something) #FILTER="|gawk '{print(tolower(\$0));}'" ##### eval "$CURLCMD \"$CURLURL\" 2>/dev/null| $XSLTCMD $XSLT - $FILTER"
Which requires this configuration file that is named weather.xslt
<!-- This XSLT is used to translate an XML response from the weather.com XML API. You can format this file to your liking. Two things you may feel like doing: 1) Modify the layout of the fields or static text already defined 2) Add other fields from the XML response file that aren't referenced in this XSLT. You can grab a full list by just doing a: wget "http://xoap.weather.com/weather/local/$LOCID?cc=*&unit=$UNITS" (change $LOCID and $UNITS to suit your needs) File modified by matthew --> <xsl:stylesheet xmlns:xsl="http://www.w3.org/1999/XSL/Transform" version="1.0" > <xsl:output method="text" disable-output-escaping="yes"/> <xsl:template match="weather"> <xsl:apply-templates select="cc"/> <xsl:apply-templates select="dayf/day@d='1'"/> </xsl:template> <xsl:template match="cc"> <xsl:value-of select="obst"/> <xsl:text> at </xsl:text><xsl:value-of select="lsup"/><xsl:text> </xsl:text> <xsl:text> Temperature: </xsl:text><xsl:value-of select="tmp"/><xsl:value-of select="/weather/head/ut"/> <xsl:if test="tmp != flik"> <xsl:text> Feels Like: </xsl:text><xsl:value-of select="flik"/><xsl:value-of select="/weather/head/ut"/> </xsl:if> <xsl:text> Conditions: </xsl:text><xsl:value-of select="t"/> <xsl:text> Wind: </xsl:text> <xsl:choose> <xsl:when test="wind/s = 'calm'"><xsl:text>0</xsl:text></xsl:when> <xsl:otherwise><xsl:value-of select="wind/s"/></xsl:otherwise> </xsl:choose> <xsl:value-of select="/weather/head/us"/> <xsl:choose> <xsl:when test="wind/s = 'calm'"><xsl:text>(0mph)</xsl:text></xsl:when> <xsl:otherwise><xsl:text> </xsl:text></xsl:otherwise> </xsl:choose> <xsl:text> (</xsl:text><xsl:value-of select="wind/t"/><xsl:text>)</xsl:text> <xsl:text> Humidity: </xsl:text><xsl:value-of select="hmid"/><xsl:text> % Barometer: </xsl:text><xsl:value-of select="bar/d"/> </xsl:template> <xsl:template match="dayf/day@d='1'"> <xsl:text> Tomorrow: </xsl:text><xsl:value-of select="low"/><xsl:value-of select="/weather/head/ut"/> <xsl:text> to </xsl:text><xsl:value-of select="hi"/><xsl:value-of select="/weather/head/ut"/> <xsl:text>, </xsl:text><xsl:value-of select="part@p='d'/t"/> <xsl:text> </xsl:text><xsl:value-of select="/weather/swa/a/t"/> <xsl:text> </xsl:text> </xsl:template> </xsl:stylesheet>
And ultimately produces output like this
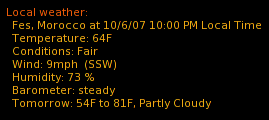
Something else that is fun is that I can run more than one instance of Conky at a time. To run both of these concurrently, I deleted the .conkyrc file and created a startup script that calls each of these configurations in separate Conky instances.
#!/bin/bash sleep 20 && exec conky -d -c ~/conky/conkyrc_main & sleep 22 && exec conky -d -c ~/conky/conkyrc_weather & exit
I have the long delay there because I call the script from GNOME (System->Preferences->Sessions, Startup Programs). The delay gives time for GNOME to get started and for my wireless ethernet connection to get set up before the script runs.
Have fun playing!
I just wanted to mention that to use the startup scripts in KDE, simply put it in the ~/.kde/Autostart and make it executable. This works great.
Joshua K: I just installed the version from the Ubuntu repos… sudo apt-get install conky. Then I created the config file(s) as noted. I didn’t bother compiling from scratch, and there isn’t much need unless you want the newest features.
Mike: Do you have curl installed? Sorry I forgot to note that. The requirement is noted in the comments in the weather script, but I forgot to note it in my blog post. It’s in the repos.
Nick & emonkey: thanks for the comments!
I heard that Conky was a real pain to install, and I was unsuccessful at my last attempt. It’s been one of the few failed attempts of anything during my experience with Ubuntu which began in January.
Any tips?
I’m getting the following error on your weather script.
XPath error : Invalid expression
dayf/day@d=’1′
^
compilation error: file /home/dbasinge/bin/weather.xslt line 24 element apply-templates
XSLT-apply-templates: could not compile select expression ‘dayf/day@d=’1”
XPath error : Invalid expression
part@p=’d’/t
^
compilation error: file /home/dbasinge/bin/weather.xslt line 59 element value-of
xsl:value-of : could not compile select expression ‘part@p=’d’/t’
compilation error: file /home/dbasinge/bin/weather.xslt line 55 element template
xsltCompilePattern : failed to compile ‘dayf/day@d=’1”
I just wanted to let everyone know that there was a great feature added to conky that is present in the gutsy version but not in feisty. It allows you to set color variables before the text. For instance, in Gutsy you can set
color0 EB5B08
then in test you just use {color0} instead of {color #EB5B08}. Then, if you ever want to change that color, you just need to change it in one place instead of everywhere. I believe you can do this for up to 5 colors.
After I’ve installed curl, it works fine here. (Kubuntu) Thanks for this nice Tip.
tgm: That is cool! Yet another reason to look forward to having time to upgrade to Gutsy! Thanks.
Chad D: Check that you have "double_buffer yes" and not "no". I know that doesn’t always work, but that’s the only thing I can think of.
Thanks for sharing. This is a really nice conky configuration and completely blows away the one I was using! I am having an issue with it going on and off though. I wouldn’t call it a flicker, but it displayed for 4 seconds then off for 4 seconds. Any idea’s what might be causing that?
greywulf: Cool! I’m glad you liked it and found it useful. I am honored. 🙂
Josh: you should be able to remove that line with no ill effects whatsoever.
I like the program. Is there any way to remove the line about my public IP address without it crashing? I am currently on Ubuntu 7.10 and I installed from the repository.
iva2k: Thanks for that. I’ve never had a problem with mine as is, but if you did, then it is likely someone else will as well. I appreciate you sharing your experience and updated file!
Great addition to conky!
I needed some fixes in weather.xslt to address the problem with error:
XSLT-apply-templates: could not compile select expression ‘dayf/day@d=’1”
Search all ‘@’ clauses and edit from
dayf/day@d=’1′
to
dayf/day[@d=’1′]
(add []’s)
see http://www.w3schools.com/xpath/x... for details.
Now it works fine. Here’s my final weather.xslt:
================================================
<!–
This XSLT is used to translate an XML response from the weather.com
XML API.
You can format this file to your liking. Two things you may feel
like doing:
1) Modify the layout of the fields or static text already defined
2) Add other fields from the XML response file that aren’t referenced in this
XSLT. You can grab a full list by just doing a:
wget "xoap.weather.com/weather/…
(change $LOCID and $UNITS to suit your needs)
File modified by matthew
–>
<xsl:stylesheet xmlns:xsl="www.w3.org/1999/XSL/Trans… version="1.0" >
<xsl:output method="text" disable-output-escaping="yes"/>
<xsl:template match="weather">
<xsl:apply-templates select="cc"/>
<xsl:apply-templates select="dayf/day[@d=’1′]"/>
</xsl:template>
<xsl:template match="cc">
<xsl:value-of select="obst"/>
<xsl:text> at </xsl:text><xsl:value-of select="lsup"/><xsl:text>
</xsl:text>
<xsl:text> Temperature: </xsl:text><xsl:value-of select="tmp"/><xsl:value-of select="/weather/head/ut"/>
<xsl:if test="tmp != flik">
<xsl:text>
Feels Like: </xsl:text><xsl:value-of select="flik"/><xsl:value-of select="/weather/head/ut"/>
</xsl:if>
<xsl:text>
Conditions: </xsl:text><xsl:value-of select="t"/>
<xsl:text>
Wind: </xsl:text>
<xsl:choose>
<xsl:when test="wind/s = ‘calm’"><xsl:text>0</xsl:text></xsl:when>
<xsl:otherwise><xsl:value-of select="wind/s"/></xsl:otherwise>
</xsl:choose>
<xsl:value-of select="/weather/head/us"/>
<xsl:choose>
<xsl:when test="wind/s = ‘calm’"><xsl:text>(0mph)</xsl:text></xsl:when>
<xsl:otherwise><xsl:text> </xsl:text></xsl:otherwise>
</xsl:choose>
<xsl:text> (</xsl:text><xsl:value-of select="wind/t"/><xsl:text>)</xsl:text>
<xsl:text>
Humidity: </xsl:text><xsl:value-of select="hmid"/><xsl:text> %
Barometer: </xsl:text><xsl:value-of select="bar/d"/>
</xsl:template>
<xsl:template match="dayf/day[@d=’1′]">
<xsl:text>
Tomorrow: </xsl:text><xsl:value-of select="low"/><xsl:value-of select="/weather/head/ut"/>
<xsl:text> to </xsl:text><xsl:value-of select="hi"/><xsl:value-of select="/weather/head/ut"/>
<xsl:text>, </xsl:text><xsl:value-of select="part[@p=’d’]/t"/>
<xsl:text>
</xsl:text><xsl:value-of select="/weather/swa/a/t"/>
<xsl:text>
</xsl:text>
</xsl:template>
</xsl:stylesheet>
================================================
Hi Josh.
What I do to accomplish both is to use a small script to start conky multiple times, using multiple configuration files. In this script you can issue a command to delay starting a specific conky instance until a certain amount of time has passed. For example, I autoload/start a file in System->Preferences->Sessions, a file I called "/home/matthew/conky/start_conky.sh". When you write yours, be sure to alter the permissions to make it executable. This is all that is in that file:
#!/bin/bashsleep 20 &&
exec conky -d -c ~/conky/conkyrc_main &
sleep 22 &&
exec conky -d -c ~/conky/conkyrc_weather &
exit
The sleep commands cause a pause, in seconds, before the next command executes. Then, I run conky twice, each time calling up a different configuration file instead of the standard .conkyrc. This file starts my main conky instance 20 seconds after it is run, and the weather instance two seconds later.
Play around with that for a while and see how you do. 🙂
O.k., I got that straightened out. Now I have a few more questions. First, How would I get conky to wait until everything else is done loading before it loads? Second how do I divide conky into separate objects on my desktop. I’ve seen it done on the Ubuntu Forums but couldn’t figure out how they were calling up the different files.
You can also use texeci (conky version 1.4.9 latest as of today) to start a separate thread for a process that takes longer.
Conky is great, thanks!
The only problem i found in gnome is when conky start’s sometimes use the fonts i choose and sometimes no..is really weird and odd.
[…] the way back in October 2007 I made two posts about conky, a lightweight and highly configurable system monitor for your […]
[…] you will recall from my earlier blog entry, I have been having fun with Conky, a lightweight system monitor that displays output to your […]